Green
Room

 |
Recent Articles |  |
- Science Killed Science Fiction
- It's a lot harder to write a sensible, up-beat science fiction adventure than it used to be, because the advance of science and technology has gotten in the way.
- Gay Marriage, Traditional Marriage, and Musical Theater
- Understanding the opposition to gay marriage with a little help from "Fiddler on the Roof."
- Screensavers Considered Harmful
- Screen savers don't save your screen. They actually shorten the lifetime of your screen, and waste power to boot. In most cases, you'd do better to disable the screen saver and tell your computer to just power down the display instead.
- Explaining Orbits with Square Planets
- physics science
- A Partial History of Computer Conferencing in Ann Arbor
- Recollections of some early on-line communities
Explaining Orbits with Square Planets
originally posted: December 19, 2007
last updated: November 11, 2013
Recently, while reading an old space adventure novel (Heinlein's The Rolling Stones) to my 8-year-old son, I paused to give a quick explanation of the basic physics of space travel to him. For part of this, I dug up an old explanation of why satellites don't fall down that I had invented long ago when I was a college student. I've always thought that this was much easier to understand than the explanations I remember from high school physics, and my son seemed to get it (even faster than I could lay it out), so I thought I'd do a little write up here. I've recently heard the process of being in an orbit described as "falling over the horizon" which is completely apt, but probably completely mysterious to the novice. This discussion should clear that up.
Preliminaries
To start with, let's review a few basic facts of physics.Suppose you are drifting around in the depths of space, far, far away from the gravitational attraction of any star or planet. You throw a ball. On the earth, if we throw a ball it starts slowing down the moment it leaves our hand, and it's path curves downward until it hits the ground. But in deep space, without the air to slow the ball down or gravity to change it's path, it would just keep moving in a straight line, at the same speed we threw it, forever. (This is Newton's first law of motion.)
Now, let's move to the surface of a planet. One without air. Now you throw your ball straight up. Because of the force of gravity, the ball will start slowing down the moment it leaves your hand. How quickly it slows down depends on how strong the gravity on the planet is. On the earth it slows down at a rate of 9.8 meters per second per second (roughly speaking, that means that every second it's speed is decreases by 9.8 meters per second). Eventually it will slow down so much that it stops, and begins to fall back down. On the way down, it speeds up at the same rate that it slowed down on the way up (9.8 meters per second per second on the Earth). So, when it comes back to your waiting hand, it will have regained all the speed it lost, and, if your hand is at the same height, the ball will hit it at the same speed you originally threw it. If you throw the ball upward at 1 mph, it lands in your hand at 1 mph. If you throw the ball upward at 100 mph, it lands in your hand at 100 mph.
For our next experiment, we'll get a bit fancier. Instead of throwing the ball straight up in the air, we'll throw it upward at an angle of 45 degrees. That is half way between straight up (90 degrees) and horizontal (0 degrees). What happens then?
This is easy to understand if we think of the ball's motion as it leaves our hand as having two parts. It has some speed upward, and some speed horizontally. If we are throwing upward at 45 degrees, then the vertical speed starts out exactly the same as the horizontal speed. We can then consider what happens to the vertical speed and horizontal speed separately.
The horizontal speed isn't effected by gravity, because gravity is vertical. So, by Newton's first law, the ball will keep moving horizontally at whatever speed I threw it, just like in our first experiment.
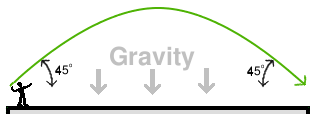
The vertical speed will behave just like our second experiment, where we threw the ball straight up. It will move upward, slowing all the time, then start moving downward, and when it returns to the level of your hand, it will have the same velocity downward that it had upward to start with. In other words, it will be moving downward at 45 degrees. The path it follows is actually a curve called a parabola, as shown in the picture below. The grey arrows show the direction of gravity, and the green curve shows the flight path of the ball.
Square Planets
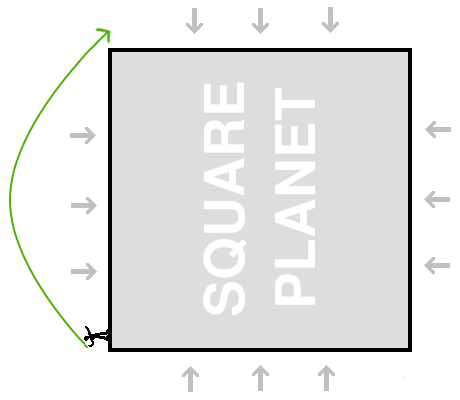
We're going to start by talking about orbits around square planets. These are completely imaginary objects that we are inventing for our temporary convience. Our square planet will look like this: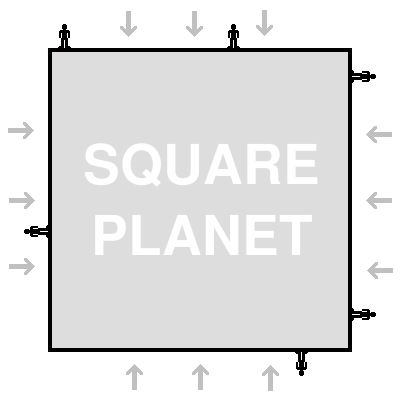
But that's not what we are going to do. Instead we're going to stand as close as we can get to one corner of the planet, and then throw our ball upward at 45 degrees, throwing it just hard enough so that it will just skim past the next corner of the planet, as shown in the picture below.
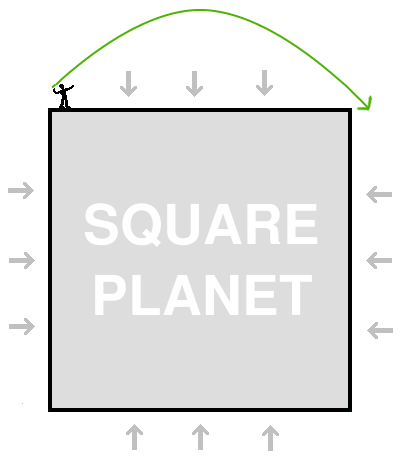
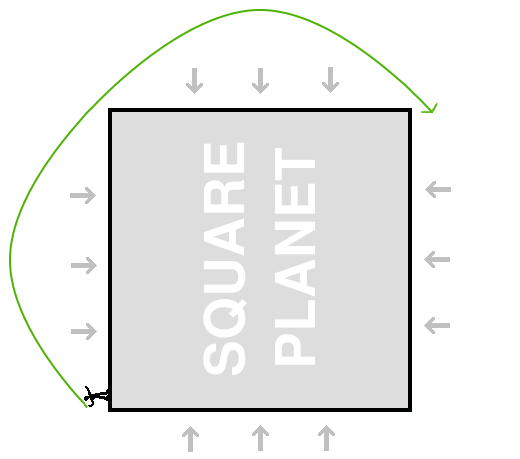
What happens next? Well, the ball is again moving at the same speed it was when we first threw it, and it is again headed 45 degrees upward, so the same thing will happen as happened when we threw it in the first place. It will fly up in a parabola, and come down at a 45 degree angle, just missing the next corner of the planet:
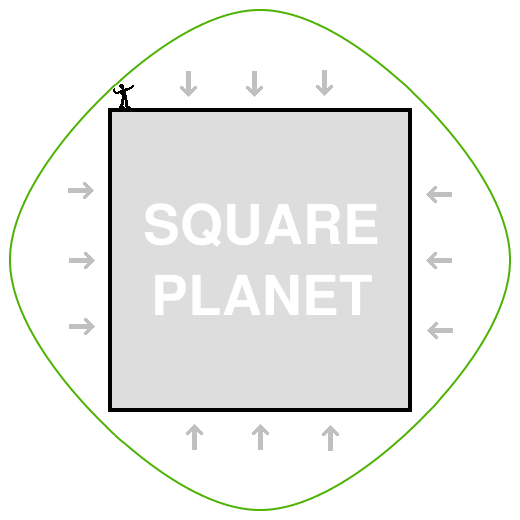
More Sides to the Story
But, of course, planets aren't really square. They're more circular.We can approach the question of circular planets by degrees though. Let's start with a hexagonal planet, a planet with six sides. Hexagons are nearer to being circular than squares. We'll make the same assumptions about gravity over each side being perpendicular to the side.
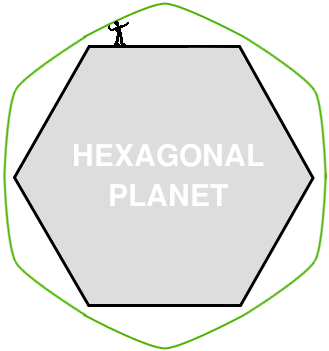
For the orbit trick to work right on a hexagonal planet, we need to throw our ball at a shallower angle than before. We know the ball will be going downward at the same angle that we launched it when it crosses the first corner. When the ball crosses that corner, we want the motion to change from the downward angle, back to the upward angle we started with. On the square planet, the direction of gravity changed by 90 degrees when we crossed from one side of the planet to the next. That was enough to change 45 degrees downward to 45 degrees upward. So 45 degrees was the magic number on the square planet. On a hexagonal planet, the direction of gravity only changes 60 degrees with each side. So on a hexagonal planet we'll launch the ball 30 degrees upward, just fast enough to miss the next corner. Crossing the corner will change the direction of "down" by 60 degrees, so our 30 degrees downward becomes 30 degrees upward and the whole orbit thing works out.
If we make n into a really, really big number, then we'll have a planet that is essentially circular. We'll be launching our ball upward at essentially zero degrees. In other words, we'll be throwing the ball straight horizontally, just fast enough that the curve downward due to gravity's pull, exactly matches the constant change in direction of gravity, and the ball travels around our perfectly circular planet in a perfectly circular orbit.